运行改动后的代码，得到下图所看到的的结果。
　　当然，这里给出的结果也是不全的，只是对说明问题没有不论什么影响。

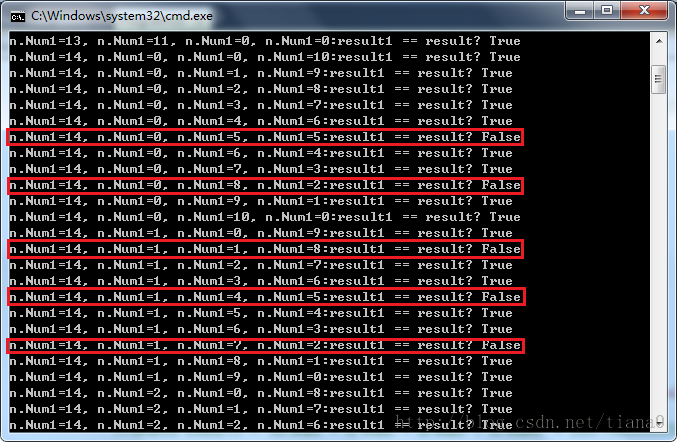
　　从图中能够看出，将整型数据换成Double型数据后，返回的结果中出现了相当数量的false，也是说result与result1不再是地相等了。我们能够通过Debug程序看看当中究竟发生了什么。 以下以图中显示的返回结果为false的第一条数据为例。看看此时的result1的值是多少，为4409.0000000000009。而result的值为4409.0，非常显然将两者进行相等比?。自然会返回false，尽管两者仅相差0.0000000000009，不相等是不相等。
　　那么，0.0000000000009的差距是如何产生的呢。
　　我们知道计算机在计算表达式“result1 = n.Num1 * 183.70833333333334  + n.Num2 * 183.70833333333334 + n.Num3 * 183.70833333333334 + n.Num4 * 183.70833333333334;”的值时。事实上会将运算分解成多步。用代码来表示其运算过程的话，应该与下面代码所看到的的运算过程类似。
　　double multi1 = n.Num1 * 183.70833333333334;
　　double multi2 = n.Num2 * 183.70833333333334;
　　double multi3 = n.Num3 * 183.70833333333334;
　　double multi4 = n.Num4 * 183.70833333333334;
　　result1 = multi1 + multi2 + multi3 + multi4;
　　而我们知道，浮点运算是不准确的，由于：计算机在处理浮点数的时候，会先把浮点数（float ， double）转换成整数再转换成二进制，然后进行操作，假设有取余，会有不同的取余方式。
　　再加上运算完毕后，将二进制转换成上层的浮点数时，又会有一些取舍。这样一来，会使终于的计算结果存在一定的误差。
　　再回到我们的问题，计算“double result = 24 * 183.70833333333334”会进行一次浮点运算。而计算“result1 = n.Num1 * 183.70833333333334+ n.Num2 * 183.70833333333334+ n.Num3 * 183.70833333333334+ n.Num4 * 183.70833333333334”时至少会进行5次浮点运算或者很多其它（这里有点拿不准）。每一次浮点运算都有可能伴随着误差的发生。所以导致终于看到的结果会随机性地产生一些偏差。
　　所以，在计算机的世界中。乘法分配律将不再适用。当然假设你对这一点点的损失无动于衷的话，你也能够觉得在计算机世界中乘法分配律相对地适应于浮点运算。
　　只是。这个问题隐藏的也太深了点吧。
　　非正确使用浮点型数据导致项目BUG了
　　在开发过程中要是没有考虑到前文所述的问题，往往会导致一些奇葩的BUG。
　　以前在项目代码中看到了与实例代码相差无几的一段代码，代码中相同使用if (result1 == result)来进行条件推断，满足此条件后再进行其它一些操作，项目上线后非常长一段时间都相安无事，突然有这段代码产生BUG了，至于BUG原因，算我不说大家也清楚。
　　后来花了非常大力气才搞清楚了问题的所在。问题弄清楚后。也才有了本文的产生。
　　所以本文作者想告诉大家：无论怎么说，开发中。在使用浮点型数据时，我们必须清楚浮点运算的特点，以免产生本文所述的类似的问题。