求极值可以使用微积分中的求极值方法，首先令Q(a，b)对a和b分别求偏导，并令偏导为零，得如下方程组：

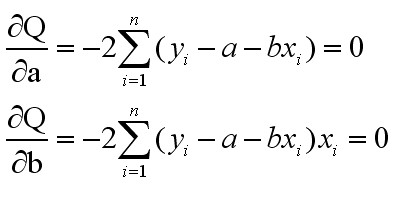
经过一系列计算和推导，终可得到:

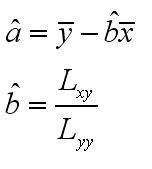
将以前的历史数据代入上述方程，可以得到a和b的小二乘估计。同样，这种机械而乏味的计算一般交由工具去完成。我用Excel得到a和b的估计分别为56.251和10.653。Excel分析结果如图3所示：

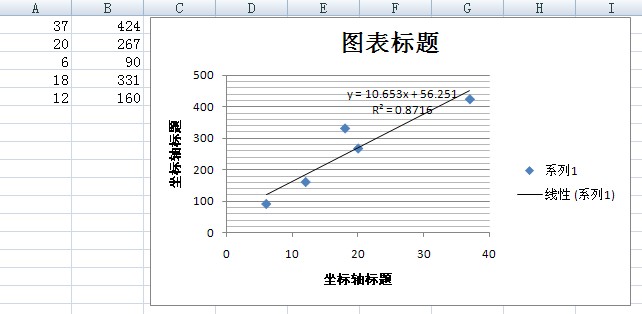
图3

根据估计结果，我们可以得出相关函数为y=56.251+10.653。我们还可以证明，这个估计是一致小方差无偏估计，证明过程从略。

现在我们不但得到了相关函数，还得到了如下有用的数据结果：这个团队在目前的管理模式下，开发一个项目平均准备时间为56.251人时，而平均每个用例开发耗时为10.653人时。

得出y

有了上面的结果，我们可以很轻易得出新项目的计划工时。例如新项目有50个用例，代入可以得到y=56.251+10.653*50=588.901，约为589个人时，再假设团队中有3个开发人员，平均每周工作五天，每天工作8小时，可以得到项目大约需要开发24.54个人日，开发周期约为5周。

后面的话

至此我们已经完成了利用一元线性回归模型对软件工期的估计。但是不得不承认，这个估计方法存在很多缺陷，如估计变量单一以及估计模型过于简单等等。实验证明，这种一元线性模型对中小型项目相对有效，如果团队比较大并且项目十分复杂，估计效果不理想了。不过这篇文章给出了一种思路，是如何利用数理统计模型以及历史经验数据来估计新项目的工期。对于文中的具体方法则可以进行诸多扩展，例如使用多个估计代理进行多元回归分析、细化估计方法等等。例如PSP中给出一种非常精细的PROBE估计法，有兴趣的朋友可以参考。另外，除了求得估计值，还可以给出估值置信区间，甚至使用蒙特卡洛模拟技术进行更复杂的分析，都可以得到更理想的估值。但是其核心思想与本文是相通的。