继上篇文章介绍完了HashMap，这篇文章开始介绍Map系列另一个比较重要的类TreeMap。 大家也许能感觉到，网络上介绍HashMap的文章比较多，但是介绍TreeMap反而不那么多，这里面是有原因：一方面HashMap的使用场景比较多；二是相对于HashMap来说，TreeMap所用到的数据结构更为复杂。 废话不多说，进入正题。
　　签名（signature）
　　public class TreeMap<K，V>
　　extends AbstractMap<K，V>
　　implements NavigableMap<K，V>， Cloneable， java.io.Serializable
　　可以看到，相比HashMap来说，TreeMap多继承了一个接口NavigableMap，也是这个接口，决定了TreeMap与HashMap的不同：
　　HashMap的key是无序的，TreeMap的key是有序的
　　接口NavigableMap
　　首先看下NavigableMap的签名
　　public interface NavigableMap<K，V> extends SortedMap<K，V>
　　发现NavigableMap继承了SortedMap，再看SortedMap的签名
　　SortedMap
　　public interface SortedMap<K，V> extends Map<K，V>
　　SortedMap像其名字那样，说明这个Map是有序的。这个顺序一般是指由Comparable接口提供的keys的自然序（natural ordering），或者也可以在创建SortedMap实例时，指定一个Comparator来决定。 当我们在用集合视角（collection views，与HashMap一样，也是由entrySet、keySet与values方法提供）来迭代（iterate）一个SortedMap实例时会体现出key的顺序。 这里引申下关于Comparable与Comparator的区别（参考这里）：
　　Comparable一般表示类的自然序，比如定义一个Student类，学号为默认排序
　　Comparator一般表示类在某种场合下的特殊分类，需要定制化排序。比如现在想按照Student类的age来排序
　　插入SortedMap中的key的类类都必须继承Comparable类（或指定一个comparator），这样才能确定如何比较（通过k1.compareTo(k2)或comparator.compare(k1， k2)）两个key，否则，在插入时，会报ClassCastException的异常。 此为，SortedMap中key的顺序性应该与equals方法保持一致。也是说k1.compareTo(k2)或comparator.compare(k1， k2)为true时，k1.equals(k2)也应该为true。 介绍完了SortedMap，再来回到我们的NavigableMap上面来。 NavigableMap是JDK1.6新增的，在SortedMap的基础上，增加了一些“导航方法”（navigation methods）来返回与搜索目标近的元素。例如下面这些方法：
　　lowerEntry，返回所有比给定Map.Entry小的元素
　　floorEntry，返回所有比给定Map.Entry小或相等的元素
　　ceilingEntry，返回所有比给定Map.Entry大或相等的元素
　　higherEntry，返回所有比给定Map.Entry大的元素
　　设计理念（design concept）
　　红黑树（Red–black tree）
　　TreeMap是用红黑树作为基础实现的，红黑树是一种二叉搜索树，让我们在一起回忆下二叉搜索树的一些性质
　　二叉搜索树
　　先看看二叉搜索树（binary search tree，BST）长什么样呢？

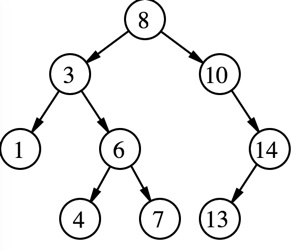
　　二叉搜索树
　　相信大家对这个图都不陌生，关键点是：
　　左子树的值小于根节点，右子树的值大于根节点。
　　二叉搜索树的优势在于每进行一次判断是能将问题的规模减少一半，所以如果二叉搜索树是平衡的话，查找元素的时间复杂度为log(n)，也是树的高度。 我这里想到一个比较严肃的问题，如果说二叉搜索树将问题规模减少了一半，那么三叉搜索树不将问题规模减少了三分之二，这不是更好嘛，以此类推，我们还可以有四叉搜索树，五叉搜索树……对于更一般的情况：
　　n个元素，K叉树搜索树的K为多少时效率是好的？K＝2时吗？
　　K 叉搜索树
　　如果大家按照我上面分析，很可能也陷入一个误区，是
　　三叉搜索树在将问题规模减少三分之二时，所需比较操作的次数是两次（二叉搜索树再将问题规模减少一半时，只需要一次比较操作）
　　我们不能把这两次给忽略了，对于更一般的情况：
　　n个元素，K叉树搜索树需要的平均比较次数为k*log(n/k)。
　　对于极端情况k＝n时，K叉树转化为了线性表了，复杂度也是O(n)了，如果用数学角度来解这个问题，相当于：
　　n为固定值时，k取何值时，k*log(n/k)的取值小？
　　k*log(n/k)根据对数的运算规则可以转化为ln(n)*k/ln(k)，ln(n)为常数，所以相当于取k/ln(k)的极小值。这个问题对于大一刚学高数的人来说再简单不过了，我们这里直接看结果
　　当k＝e时，k/ln(k)取小值。
　　自然数e的取值大约为2.718左右，可以看到二叉树基本上是这样优解了。在Nodejs的REPL中进行下面的操作
　　function foo(k) {return k/Math.log(k);}
　　> foo(2)
　　2.8853900817779268
　　> foo(3)
　　2.730717679880512
　　> foo(4)
　　2.8853900817779268
　　> foo(5)
　　3.1066746727980594