第二步：计算圈复杂度

　　圈复杂度是一种为程序逻辑复杂性提供定量测度的软件度量，将该度量用于计算程序的基本的独立路径数目，为确保所有语句至少执行一次的测试数量的上界。独立路径必须包含一条在定义之前不曾用到的边。

　　有以下三种方法计算圈复杂度：

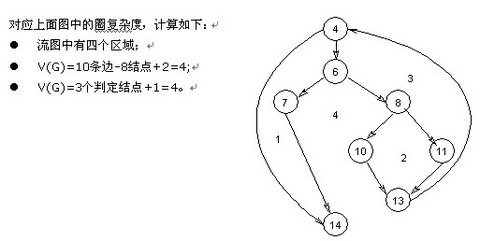
　　流图中区域的数量对应于环型的复杂性;

　　给定流图G的圈复杂度V(G)，定义为V(G)=E-N+2，E是流图中边的数量，N是流图中结点的数量;

　　给定流图G的圈复杂度V(G)，定义为V(G)=P+1，P是流图G中判定结点的数量。

　　第三步：导出测试用例

　　根据上面的计算方法，可得出四个独立的路径。(一条独立路径是指，和其他的独立路径相比，至少引入一个新处理语句或一个新判断的程序通路。V(G)值正好等于该程序的独立路径的条数。)

　　路径1：4-14

　　路径2：4-6-7-14

　　路径3：4-6-8-10-13-4-14

　　路径4：4-6-8-11-13-4-14

　　根据上面的独立路径，去设计输入数据，使程序分别执行到上面四条路径。

　　第四步：准备测试用例

　　为了确保基本路径集中的每一条路径的执行，根据判断结点给出的条件，选择适当的数据以保证某一条路径可以被测试到，满足上面例子基本路径集的测试用例是：

　　举例说明：

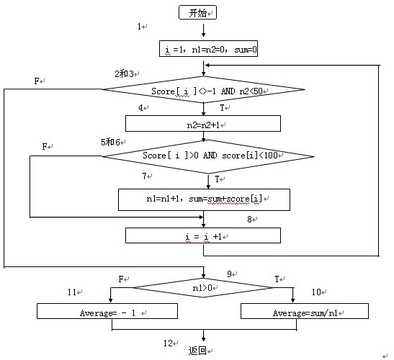
　　例：下例程序流程图描述了多输入50个值(以–1作为输入结束标志)，计算其中有效的学生分数的个数、总分数和平均值。