将这100个区间的样本数标注在十字坐标系上：

　　这个图不禁让人想起了令人泪流满面的正态分布，虽然我想避免描述这个晦涩拗口的数学名词，但现在看来躲避这个礁石并不是一个好主意。

　　为了避免本文被读者直接打入冷宫，我打算尽量少用公式，因此下面这幅正态分布密度函数图我先列了出来：

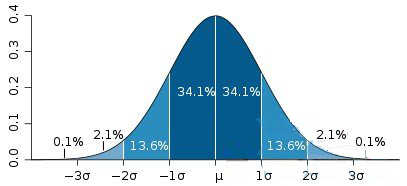
　　X轴的坐标正是前面提到过的Z值，当Z=3的时候，我们从上图可以看到，正态函数所覆盖的面积达到了99.73%。X轴的单位  则是上面提到过的总体标准差。这种曲线特征恰好与我上面的例子所绘出的图形有不谋而合之处，正态分布的意义恰在于此，它为我们的测试数据提供了强有力的数学依据，告诉我们这些测试数据说明了什么，为什么会这样。本文侧重点不在正态分布的介绍和推导上，但是首先我将检验上面这个例子中的样本数是符合正态分布的。

　　对于样本的正态分布检验有多种方法，如假设检验、Jarque-Bera检验等等，这里为了简单起见，我将使用常见的假设检验。

　　样本数据  是总体  的样本，假设检验的前提是假设总体是符合正态分布的，  分别是其样本均值和样本方差。由表中列举的数据可以计算出：  ，  。假设样本总体均值为  （这里总体均值用样本标准偏差代替），拒绝域  。假设显著性  ，查表得到 ，所以  ，因此上述分布是显著的正态分布。这里拒绝域  的含义可以从下图中理解：