3) 使用Rayleigh曲线来建模软件开发质量涉及两个假设：

在开发过程中观察到的缺陷率与应用中的缺陷率成正比关系。对应于图1来说，也是如果开发过程中观测到的缺陷率越高，CDF中图的幅度越高，K值越大；

给定同样的错误植入率，假如更多的缺陷被发现并更早将其移出，那么在后期阶段遗留的缺陷更少，应用领域的质量更好。对应于图2来说，曲线与X、Y轴围成区域的面积是一定的（总的缺陷数是确定的），如果在前期移除较多缺陷，即曲线的峰值点前移，那么后期曲线的面积会小，代表后期遗留的缺陷数减少。

4) 使用场景：收集数据应当越早越好；且需要持续的追踪缺陷数。

5) 优势：随时间信息的缺陷密度可预测，因此在测试阶段使得找到并验证缺陷的估计成为可能。

6) Rayleigh模型没有考虑到变化调整的机制，所以可能会影响到缺陷的预测。

2. 指数模型

指数模型是针对测试阶段，尤其是验收类测试阶段的缺陷分布的模型，其基本原理是在这个阶段出现的缺陷（或者失效模式，我们这里讨论的是缺陷）是整个产品可靠性的良好指证。它是Weibull系列的另一个特例。指数模型是许多其他可靠性增长模型的基础。指数模型可分为故障/失效计数模型(fault/failure count model)和失效间隔时间模型(time between failures model)。基本的指数模型的累积缺陷分布函数(CDF)为y=K*a*b^t，修正指数模型在基本指数模型曲线函数上加一个常数因子。

1) 指数模型的函数形式

指数模型的累积缺陷分布函数(CDF)：F(t)=K*(1-exp(-λ*t))；

指数模型的缺陷概率密度函数(PDF)：f(t)=K*(λ*exp(-λ*t))。

其中，t是时间，K是总缺陷数，λ与K是需要估计的两个参数。

2) 指数模型对应的函数图

图3 指数模型的CDF图

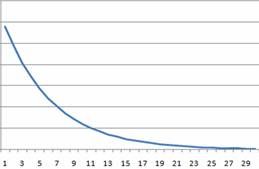
图4 指数模型的PDF图

2) 指数模型的关键假设：测试工作量在测试阶段中是均匀的。

3) 使用：指数模型预测缺陷时是基于正式的测试阶段的数据的，因此它主要适用于这些阶段，好在开发过程后期??例如后的测试阶段。但在交付用户使用后，用户发现的缺陷模型，与交付用户之前的模型往往有很大差别，这是由于交付客户后影响客户的测试的不确定因素更多。

4) 优势：简单有用的模型之一，易于使用和实现。

5) 缺陷：假设测试的工作量在整个测试阶段是均匀的。

3. NHPP模型（非齐次泊松过程模型）

NHPP模型是对在给定间隔内观察到的故障数建模，它是指数模型的一个直接应用。

1) NHPP模型的函数形式：其中，参数的含义与指数模型相同

NHPP模型的累积缺陷分布函数(CDF)：F(t)=K*(1-exp(-λ*t))；

NHPP模型的缺陷概率密度函数(PDF)：f(t)=K*λ*c^(-λ*t)。

2) NHPP模型对应的函数图：见指数模型

3) 由于NHPP模型是指数模型的应用，所以NHPP 模型的特征与指数模型的特征相同。

4) 缺陷：大多数NHPP模型都基于这样的假设：每个缺陷的严重性和被监测到的可能性相同，在排除一个缺陷时不引入另一个新的缺陷，但实际情况并非如此。缺陷之间是存在着关联关系的。

4. S型可靠性增长模型

S型增长模型是软件领域应用较为广泛的模型之一，下一篇，将会详细进行介绍。