成长曲线
终于要介绍到预测方法啦。有了前面两篇文章的基础，大家应该都对预测有了认识。还是那句话，知道了要做什么，接下来该想要“怎么做”。明白了预测的重要性，那该去想想，怎么去预测？不过别心急，我们一步一步来，这篇文章会介绍预测工具的基础知识??成长曲线。

什么是成长曲线？成长曲线是描绘观测样本从初始阶段不断发展壮大所经历的全部过程的曲线。在软件领域的成长曲线的过程中，要观测的样本值会经历萌芽、发展、稳定等阶段。成长曲线在很多方面都有应用，比如在报纸上、经济类刊物上常常能看到的经济成长曲线、品牌成长曲线；再比如细心的妈妈都会把宝宝出生后的成长情况记录下来，绘成儿童成长曲线等等。

在软件领域中同样有成长曲线，软件领域中的成长曲线反映了软件系统中的要观测的某个属性随着各种因素（如时间、成本等）变化发展的情况。成长曲线可以拟合事物发展的趋势，曲线拟合（Curve fitting）是用连续曲线近似地刻画或比拟平面上离散的点表示的坐标之间的函数关系的一种数据处理方法。在数值分析中，曲线拟合是用解析表达式逼近离散数据，即离散数据的公式化，是选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两变量间的关系。

接着回到软件领域中的成长曲线上。对于一个系统来说，进入开发阶段后，开发人员每天都要完成一定量的代码行，而代码行的总数在项目计划阶段应当是估算好的，那么，开发人员应当按照怎样的速度完成这些代码；已经完成了一部分代码后，能否判断出这样的速度是否合理、能否按期完成任务；前期完成过多代码可能会造成后期工作量太小，而前期完成太少代码又可能会带来后期的工作繁重。也许这时，你会迫切需要一个工具来对开发人员的工作进行监控。进入测试阶段也是一样。所以这里提到的软件领域中的成长曲线的预测，是针对软件的开发阶段和测试阶段的。再以测试为例，成长曲线能够反映缺陷从初的测试出的缺陷较少，到中期不断发展增多，再到终测出的缺陷数稳定不变的全部过程。成长曲线应当是连续的，它能够表示一段时间内事物持续发展的情况，能够表示事物在一个持续的时间段内发展的全过程。

成长曲线有很多种形式。常见的线性曲线也可以看作是成长曲线的一种，只是在现实中，线性曲线的使用不如非线性曲线广泛。下面将几种常见的成长曲线归纳介绍，希望对大家的理解有所帮助。

1. Rayleigh模型

Rayleigh模型是Weibull分布的一种特殊形式，是一种常用的模型。Weibull分布重要的一个特征是它的概率密度函数的尾部逐渐逼近0，但永远达不到0，在许多工程领域都使用了很多年。Rayleigh模型既可以对软件开发全生命周期进行预测，也可以仅对测试阶段的缺陷分布进行预测，得到所期望的时间间隔t与所发现缺陷的关系。对于成熟的组织，当项目周期、软件规模和缺陷密度已经确定时，可以得到确定的缺陷分布曲线，并可以据此控制项目过程的缺陷率。如果项目进行中实际的缺陷值与预估的缺陷值有较大差别时，说明中间出现问题，需要加以控制。

1) Rayleigh模型的函数形式

Rayleigh模型的累积分布函数(CDF)：F(t)=K*(1-exp^(-(t/c)^2))；

Rayleigh模型的概率密度函数(PDF)：f(t)=2*K*t/(c^2)*( exp^(-(t/c)^2))。

上面两个函数中，t是时间自变量，c是一个常量(c=2^(1/2)tm，tm是f(t)到达峰值对应的时间)，K是曲线与坐标形成的面积（总缺陷数），也是我们要估计的参数。多年的预测经验得到缺陷在tm时间的比率(F(tm)/K)约等于0.4，即在f(t)到达大值时，已出现的缺陷大约占总缺陷的40%。按照这个推导，在某一时间可以估算出总的缺陷数以及具体的Rayleigh分布参数，从而将缺陷的计算过程简化。

2) Rayleigh函数对应的图

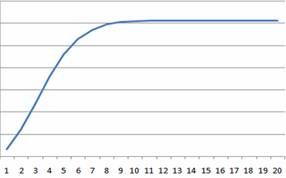
图1 Rayleigh模型的CDF图

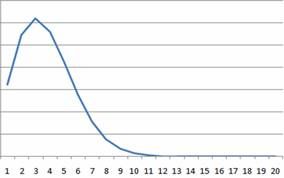
图2 Rayleigh模型的PDF图

由图1??CDF图可以看出，累积密度终趋近一个大值（K）；由图2??PDF图可以看出，缺陷随时间逐渐降低终趋向于0。