关于AVL树的简介可以参考： 数据结构与算法——AVL树简介
　　关于二叉搜索树（也称为二叉查找树）可以参考：数据结构与算法——二叉查找树类的C++实现
　　AVL-tree是一个"加上了额外平衡条件"的二叉搜索树，其平衡条件的建立是为了确保整棵树的深度为O(logN)。要求任何节点的左右子树高度相差多1。
　　该AVL树结点的数据结构:
　　struct AvlNode{
　　Comparable element;
　　AvlNode * left;
　　AvlNode * right;
　　int height;
　　AvlNode(const Comparable & e， AvlNode * lt， AvlNode * rt， int h = 0):element(e)， left(lt)， right(rt)， height(h){}
　　};
　　该结点数据结构其实是一个结点类。
　　该AVL树的主要成员函数：
　　void makeEmpty();//清空该树
　　bool isEmpty() const;//判断该树是否为空
　　void lessOrderPrintTree();//从小到大输出该AVL平衡树
　　void biggerOrderPrintTree();//从大到小输出该AVL平衡树
　　void insert(const Comparable & x);//插入值为x的结点
　　Comparable findMin() const;//找到小值
　　Comparable findMax() const;//找到大值
　　主要成员函数介绍：
　　/****************************************************************
　　*   函数名称：void insert(const Comparable & x， AvlNode * t)
　　*   功能描述: 在结点t的后面插入值为x的结点
　　*   参数列表: x为要插入结点的值
　　*             t为当前的结点
　　*   返回结果：void
　　*****************************************************************/
　　template<typename Comparable>
　　void AvlTree<Comparable>::insert(const Comparable & x， AvlNode * & t)
　　{
　　if(t == NULL)//当前结点为空
　　t = new AvlNode(x， NULL， NULL);
　　else if(x < t->element){
　　insert(x， t->left);
　　if(height(t->left) - height(t->right) == 2){
　　if(x < t->left->element)//单旋转，左左插入
　　rotateWithLeftChild(t);
　　else
　　doubleWithLeftChild(t);//双旋转，左右插入
　　}
　　}
　　else if(x > t->element){
　　insert(x， t->right);
　　if(height(t->right) - height(t->left) == 2){
　　if(x > t->right->element)//单旋转，右右插入
　　rotateWithRightChild(t);
　　else
　　doubleWithRightChild(t);//双旋转，右左插入
　　}
　　}
　　//如果x的值和当前结点的值相同，则忽略。也可以向之前二叉查找树一样给每个结点再加一个num成员变量。
　　t->height = max(height(t->left)， height(t->right)) + 1;//更新结点t的高度
　　}
　　/****************************************************************
　　*   函数名称：rotateWithLeftChild(AvlNode *t)
　　*   功能描述: 将当前结点进行单旋转，用于左左插入的时候
　　*   参数列表: t是指向当前结点的指针
　　*   返回结果：无
　　*****************************************************************/
　　template<typename Comparable>
　　void AvlTree<Comparable>::rotateWithLeftChild(AvlNode * & k2)
　　{
　　cout << "左单旋转" << endl;
　　AvlNode * k1 = k2->left;
　　k2->left = k1->right;
　　k1->right = k2;
　　k2->height = max(height(k2->left)， height(k2->right)) + 1;
　　k1->height = max(height(k1->left)， k2->height) + 1;
　　k2 = k1;
　　}
　　/****************************************************************
　　*   函数名称：rotateWithRightChild(AvlNode *t)
　　*   功能描述: 将当前结点进行单旋转，用于左右插入的时候
　　*   参数列表: t是指向当前结点的指针
　　*   返回结果：无
　　*****************************************************************/
　　template<typename Comparable>
　　void AvlTree<Comparable>::rotateWithRightChild(AvlNode * & k1)
　　{
　　cout << "右单旋转" << endl;
　　AvlNode * k2 = k1->right;
　　k1->right = k2->left;
　　k2->left = k1;
　　k1->height = max(height(k1->left)， height(k1->right)) + 1;
　　k2->height = max(height(k2->right)， k1->height) + 1;
　　k1 = k2;
　　}
　　/****************************************************************
　　*   函数名称：doubleWithLeftChild(AvlNode *t)
　　*   功能描述: 将当前结点进行双旋转，用于左右插入的时候
　　*   参数列表: t是指向当前结点的指针
　　*   返回结果：无
　　*****************************************************************/
　　template<typename Comparable>
　　void AvlTree<Comparable>::doubleWithLeftChild(AvlNode * & k3)
　　{
　　cout << "**********************" << endl;
　　cout << "左双旋转: " << endl;
　　rotateWithRightChild(k3->left);
　　rotateWithLeftChild(k3);
　　cout << "**********************" << endl;
　　}
　　/****************************************************************
　　*   函数名称：doubleWithRightChild(AvlNode *t)
　　*   功能描述: 将当前结点进行双旋转，用于右左插入的时候
　　*   参数列表: t是指向当前结点的指针
　　*   返回结果：无
　　*****************************************************************/
　　template<typename Comparable>
　　void AvlTree<Comparable>::doubleWithRightChild(AvlNode * & k1)
　　{
　　cout << "**********************" << endl;
　　cout << "右双旋转: " << endl;
　　rotateWithLeftChild(k1->right);
　　rotateWithRightChild(k1);
　　cout << "**********************" << endl;
　　}
　　关于右单旋转的一个图例：

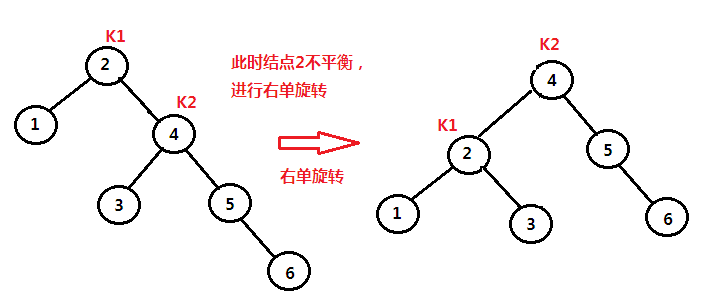
　　数据结构与算法AVL树类的C++实现template<typename Comparable> void AvlTree<Comparable>::rotateWithRightChild(AvlNode * & k1) { cout << "右单旋转" << endl; AvlNode * k2 = k1->right; k1->right = k2->left; k2->left = k1; k1->height = max(height(k1->left)， height(k1->right)) + 1; k2->height = max(height(k2->right)， k1->height) + 1; k1 = k2; }左单旋转是同样的道理。
　　关于右双旋转的一个图例：

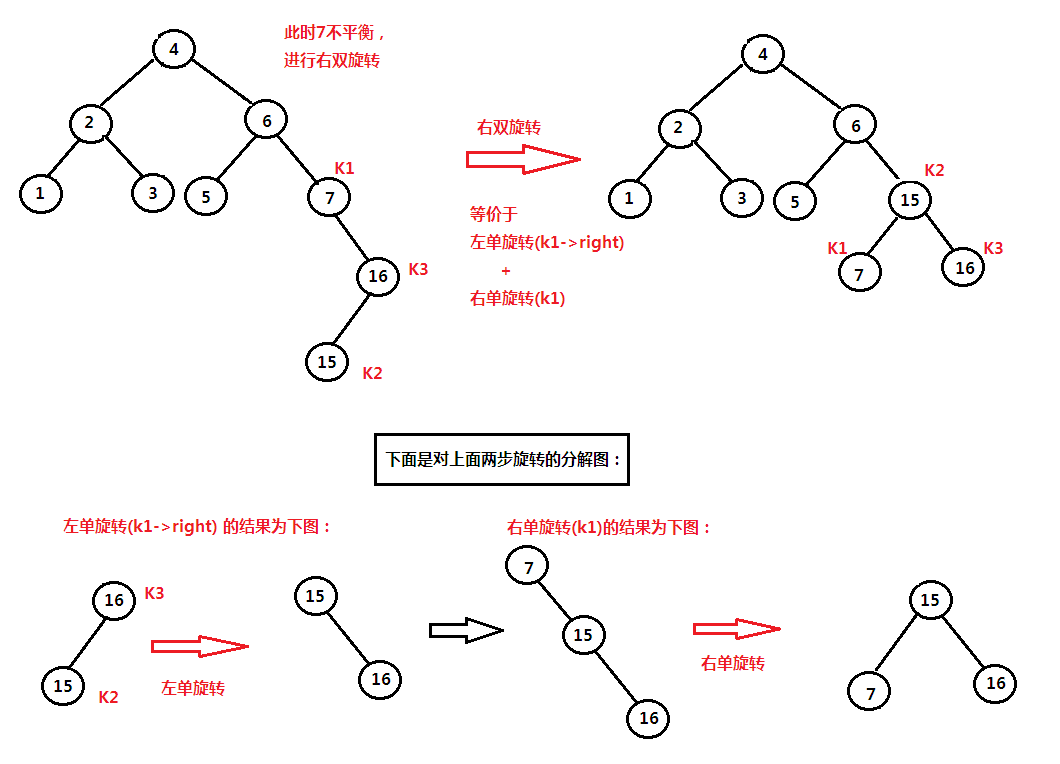
　　template<typename Comparable> void AvlTree<Comparable>::doubleWithRightChild(AvlNode * & k1) { cout << "**********************" << endl; cout << "右双旋转: " << endl; rotateWithLeftChild(k1->right); rotateWithRightChild(k1); cout << "**********************" << endl; }
　　该函数中的注释是为了测试该函数是否执行了。
　　下面给出一个完整的实测：
　　依次向树中插入结点: 1， 2， 3， 4， 5， 6， 7， 16， 15。
　　先用图示来表现一下具体的实现过程，然后用程序来验证一下。在main函数的tree2树是用该数据序列生成的AVL树，可以看打印信息是否经过了相应的旋转。

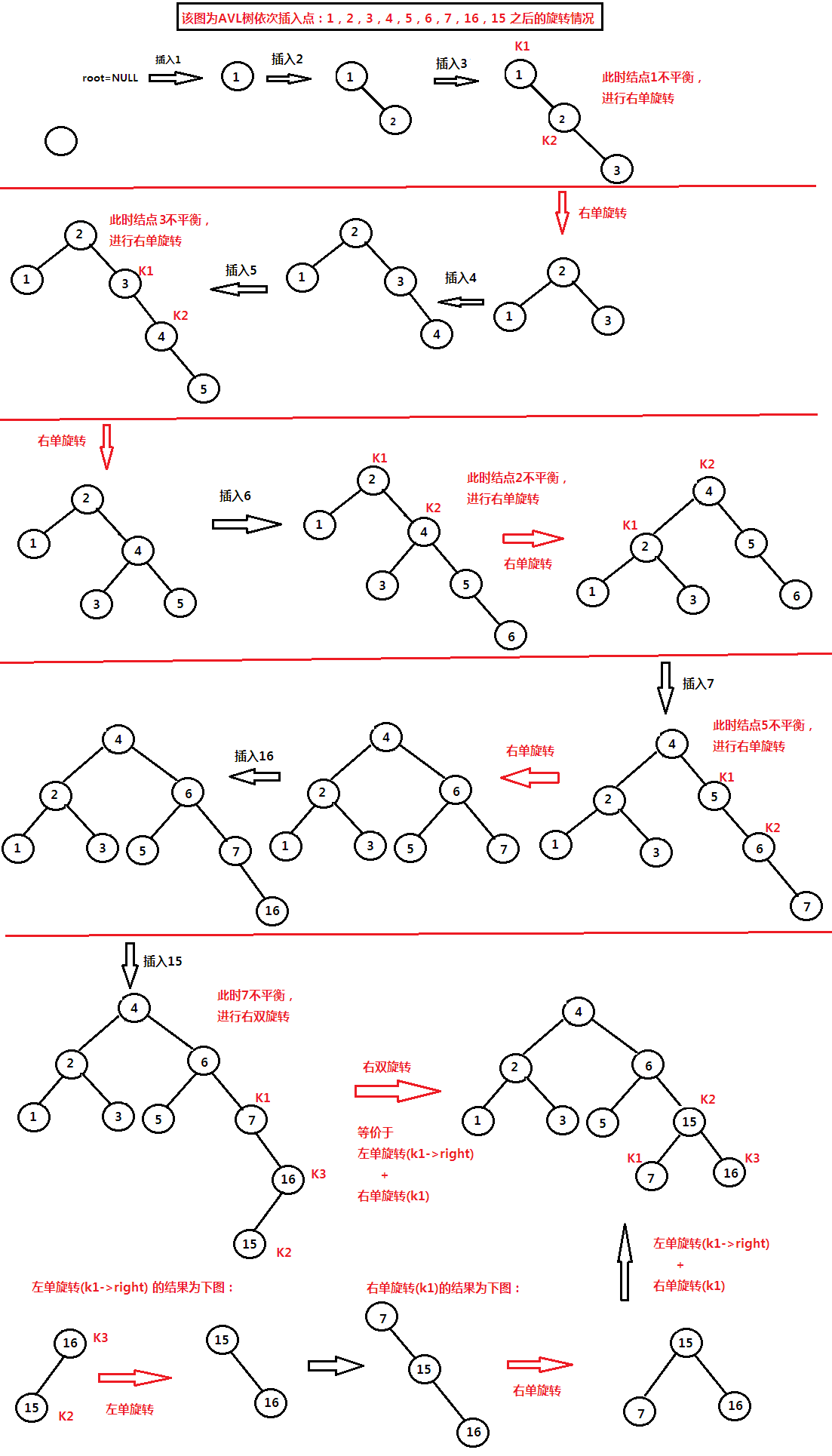
　　AvlTree<int> tree2; cout << "构造AVL树trre2: " << endl; for(int i = 1; i < 8; ++i) tree2.insert(i); tree2.insert(16); tree2.insert(15); tree2.lessOrderPrintTree(); tree2.biggerOrderPrintTree();输出为：
　　构造AVL树trre2:
　　右单旋转
　　右单旋转
　　右单旋转
　　右单旋转
　　**********************
　　右双旋转:
　　左单旋转
　　右单旋转
　　**********************
　　从小到大输出：1 2 3 4 5 6 7 15 16
　　从大到小输出：16 15 7 6 5 4 3 2 1
　　下面是该AVL树类的源代码：
　　/*************************************************************************
　　> File Name: AvlTree.cpp
　　> Author:
　　> Mail:
　　> Created Time: 2016年04月08日 星期五 10时14分48秒
　　************************************************************************/
　　#include <iostream>
　　#include <algorithm>
　　#include <vector>
　　using namespace std;
　　template<typename Comparable>
　　class AvlTree{
　　public:
　　AvlTree(){ root = NULL; }
　　~AvlTree();
　　void makeEmpty();//清空该树
　　bool isEmpty() const;//判断该树是否为空
　　void lessOrderPrintTree();//从小到大输出该AVL平衡树
　　void biggerOrderPrintTree();//从大到小输出该AVL平衡树
　　void insert(const Comparable & x);//插入值为x的结点
　　Comparable findMin() const;//找到小值
　　Comparable findMax() const;//找到大值
　　private:
　　struct AvlNode{
　　Comparable element;
　　AvlNode * left;
　　AvlNode * right;
　　int height;
　　AvlNode(const Comparable & e， AvlNode * lt， AvlNode * rt， int h = 0):element(e)， left(lt)， right(rt)， height(h){}
　　};
　　AvlNode * root;
　　private:
　　void makeEmpty(AvlNode * t);
　　void lessOrderPrintTree(AvlNode * t);
　　void biggerOrderPrintTree(AvlNode * t);
　　int height(AvlNode * t) const;//获得当前结点t的高度
　　void insert(const Comparable & x， AvlNode * & t);//在t处，插入值为x的结点
　　void rotateWithLeftChild(AvlNode * & k2);//单旋转，左左插入的情况
　　void rotateWithRightChild(AvlNode * & k1);//单旋转，右右插入的情况
　　void doubleWithLeftChild(AvlNode * & k3);//双旋转，左右插入的情况
　　void doubleWithRightChild(AvlNode * & k1);//双旋转，右左插入的情况
　　Comparable findMin(AvlNode * t) const;//找到小值
　　Comparable findMax(AvlNode * t) const;//找到大值
　　};