1.引言
　　矩阵分解(MatrixFactorization，MF)是传统推荐系统为经典的算法，思想来源于数学中的奇异值分解(SVD)，但是与SVD还是有些不同，形式可以看出SVD将原始的评分矩阵分解为3个矩阵，而推荐本文要介绍的MF是直接将一个矩阵分解为两个矩阵，一个包含Users的因子向量，另一个包含着Items的因子向量。
　　2.原理简介
　　假如电影分为三类：动画片，武打片，纪录片，而某一部电影对应这三类的隶属度分别为0，0.2，0.7，可以看出这是一部纪录片里面有些武打成分，现在给定某个用户对着三类电影的喜欢程度用0到1之间的值表示分别为0.1，0.6，0.2，可以看出该用户喜欢武打片，而不怎么喜欢其他两种，于是可以预测用户对刚才的电影打分（喜欢程度）为：0*0.1+0.2*0.6+0.7*0.2=0.26
　　矩阵分解的动机来源于此，因为利用用户的历史评分矩阵（参考我的上一篇推荐系统之协同过滤的原理及C++实现），如果能够得到反映每一用户的对每个Item喜好的因子向量，同时得到每个Item属于每一类的隶属度向量，利用上面的方法很容易得出每个用户对每个Item的预测评分，利用这个评分的高低可以进行推荐高分的Items给相应的用户了.

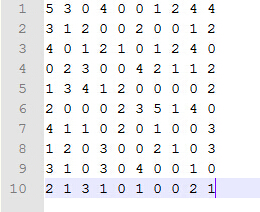
　　例如这个10*10的历史评分矩阵A，可以分解为一个10*5的矩阵B乘以一个5*10的矩阵C，这样可以把B看做是用户偏好矩阵，里面包含着用户对每一类Items的偏好程度的向量，B的转置看作是包含着衡量每一个Item属于5类的隶属度的向量，当然这个5可以是自己设定的任意值，但是原则上要求要比原来的矩阵A中的列数或者行数小，起到一个降维的作用。B和C的初始值可以随机初始化，然后B和C相乘得到评分，与历史真实评分对比，通过梯度下降算法不断调整B和C中的值，使得B和C相乘后得到的矩阵与真实的历史评分矩阵之间的差别越小越好，终得到较好的B和C可以用来预测用户对任意Item的评分了，更加详细的解释参考：Matrix_factorization_techniques_for_recommender_systems.pdf
　　3.实现
　　本次实现的是一个带偏置的矩阵分解，数据集是movielens.rar，已经处理成了矩阵形式
　　读取和保存txt数据的头文件
1#ifndefREADANDWRITEDATA_H
2#defineREADANDWRITEDATA_H
3#include<iostream>
4#include<fstream>
5#include<vector>
6#include<string>
7
8usingnamespacestd;
9
10template<typenameT>
11vector<vector<T>>txtRead(stringFilePath，introw，intcol)
12{
13ifstreaminput(FilePath);
14if(!input.is_open())
15{
16cerr<<"Fileisnotexisting，checkthepath: "<<FilePath<<endl;
17exit(1);
18}
19vector<vector<T>>data(row，vector<T>(col，0));
20for(inti=0;i<row;++i)
21{
22for(intj=0;j<col;++j)
23{
24input>>data[i][j];
25}
26}
27returndata;
28}
29
30template<typenameT>
31voidtxtWrite(vector<vector<T>>Matrix，stringdest)
32{
33ofstreamoutput(dest);
34vector<vector<T>>::size_typerow=Matrix.size();
35vector<T>::size_typecol=Matrix[0].size();
36for(vector<vector<T>>::size_typei=0;i<row;++i)
37{
38for(vector<T>::size_typej=0;j<col;++j)
39{
40output<<Matrix[i][j];
41}
42output<<endl;
43}
44}
45#endif