6.示例1
　　给出三个任意正数a、b、c判断其能否构成三角形及三角形按边分类的类型
　　1、 确定规则的个数，先定义条件个数，如下：
　　三角形按照边分为：等腰三角形、等边三角形、一般三角形
　　根据分析，确定条件如下：
　　a<b+c、b<a+c、c<a+b、a=b、b=c、c=a，故规则的个数有2的6次方64个
　　2、初始判定表

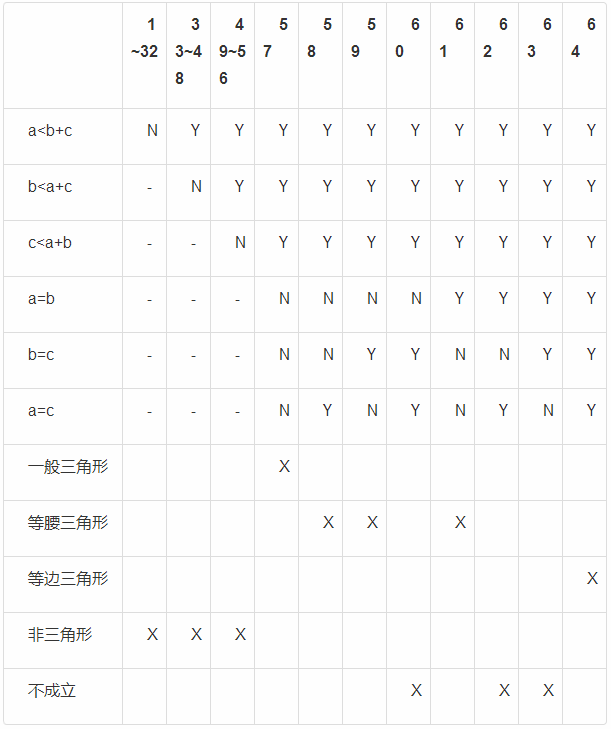
　　上述判定表已经是合并相同规则后的表格，经过简化后（去除不可能条件）得到终判定表如下：

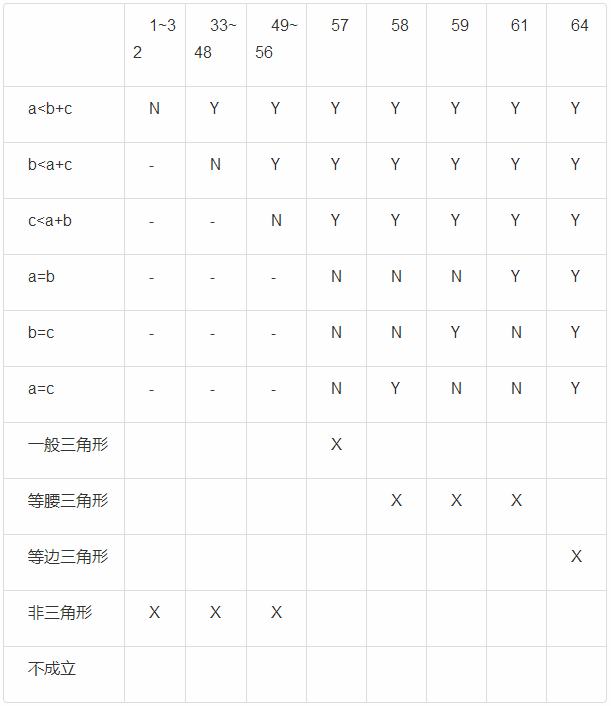
　　根据上述判定表，得到用例如下：

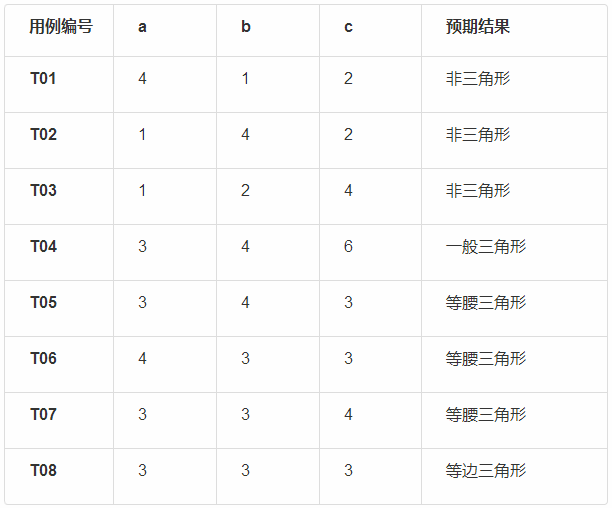
　　7.示例2
　　主持人对甲、乙、丙三人说：“这里有三顶红帽子，两顶白帽子。现在用布蒙上你们的眼睛，给你们每人戴上一顶帽子，然后请你们依次睁开眼睛，能正确说出自己所戴帽子的颜色者有奖。”
　　带完帽子后，甲拿下布后看了其他两人的帽子说：“我不知道。”
　　然后，乙解开布看了其他两人的帽子后说：“我不知道。”
　　轮到丙时，他没有拿下布正确地说出了自己所戴帽子的颜色。
　　试问：丙戴的是什么帽子？他是怎样得出结论的？

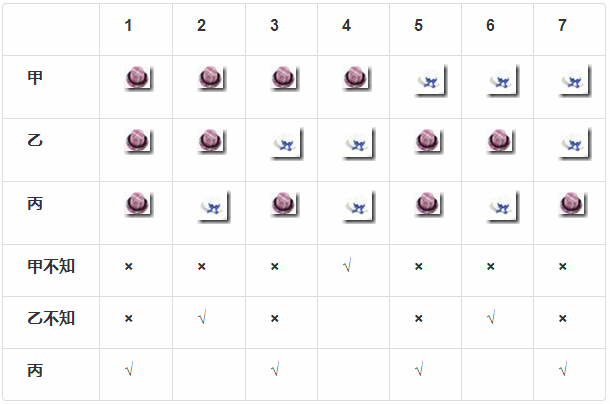
　　由上述判定表可知，所有符合题干假设的，只有1、3、5、7满足条件，而满足条件的所有组合中，丙均为红色莫阿紫，故而得出结论