C++二叉查找树实现过程详解

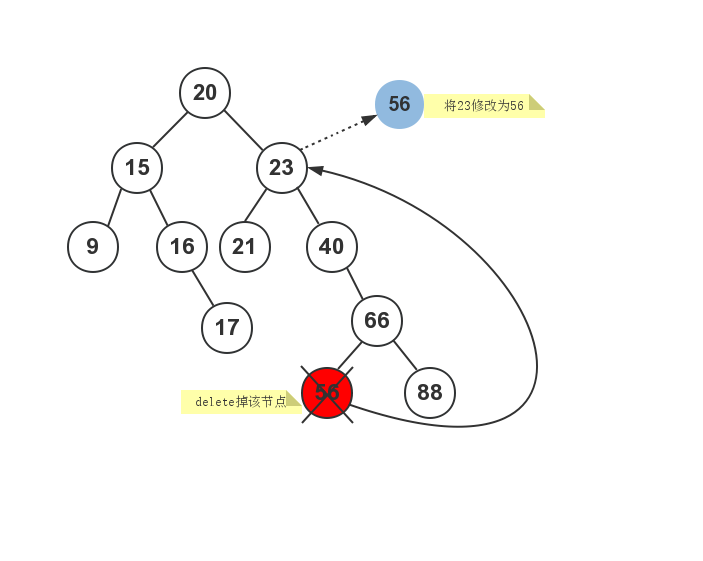
　　代码实现如下：
　　template<class T>
　　void BinarySearchTree<T>::remove(const T &x， BinaryNode<T> *&t) const
　　{
　　if (t == NULL)
　　{
　　return;
　　}
　　if (x < t->element)
　　{
　　remove(x， t->left);
　　}
　　else if (x > t->element)
　　{
　　remove(x， t->right);
　　}
　　else if (t->left != NULL && t->right != NULL)
　　{
　　// 拥有两个子节点
　　t->element = findMin(t->right)->element;
　　remove(t->element， t->right);
　　}
　　else if (t->left == NULL && t->right == NULL)
　　{
　　// 没有子节点，直接干掉
　　delete t;
　　t = NULL;
　　}
　　else if (t->left == NULL || t->right == NULL)
　　{
　　// 拥有一个子节点
　　BinaryNode *pTemp = t;
　　t = (t->left != NULL) ? t->left : t->right;
　　delete pTemp;
　　}
　　}
　　makeEmpty实现
　　makeEmpty函数用来释放整个二叉查找树占用的内存空间，同理，也是使用的递归的方式来实现的。具体代码请下载文中后提供的源码。
　　总结
　　这篇文章对数据结构中非常重要的二叉查找树进行了详细的总结，虽然二叉查找树非常重要，但是理解起来还是非常容易的，主要是需要掌握对递归的理解。如果对递归有非常扎实的理解，那么对于树的一些操作，那都是非常好把握的，而理解二叉查找树又是后续的AVL平衡树和红黑树的基础，希望这篇文章对大家有帮助。