其基本模式如下：

　　分解：把一个问题分解成与原问题相似的子问题

　　解决：递归的解各个子问题

　　合并：合并子问题的结果得到了原问题的解。

　　现在用递归算法，采用上面的分治思想来解合并排序。

　　合并排序（非降序）

　　分解：把合并排序分解成与两个子问题

　　伪代码：

    MERGE_SORT(A， begin， end)
    if begin < end
       then mid<- int((begin + end)/2)
               MERGE_SORT(A， begin， mid)
               MERGE_SORT(A， mid+1， end)
               MERGE(A， begin， mid， end)

　　解决：递归的解各个子问题，每个子问题又继续递归调用自己，直到"begin<end"这一条件不满足时，即"begin==end"时，此时只有一个元素，显然是有序的，这样再进行下一步合并。

　　合并：合并的子问题的结果有个隐含问题，即各个子问题已经是排好序的了（从两个氮元素序列开始合并）。做法是比较两个子序列的第一个元素小的写入终结果，再往下比较，如下图所示：

　　图中：待排序数组为2 4 6  1 3 5

　　把2 4 6和 1 3 5 分别存到一个数组中，比较两个数组的第一个元素大小小者存于大数组中，直到两小数组中元素都为32767.

　　这里32767 味无穷大，因为c语言中int类型是32位，表示范围是-32768-----32768。用无穷大作为靶子可以减少对两个小数组是否为空的判断，有了靶子，直接判断大数组元素个数次排完了。

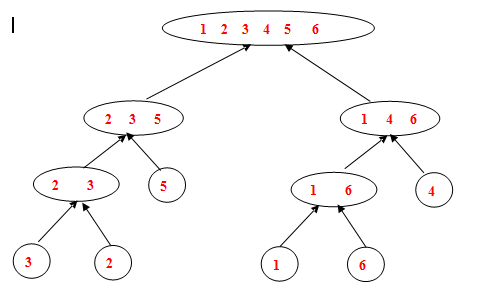
　　在整个过程中执行过程示如下图：