正交矩阵测试策略Orthogonal Array Testing Strategy (OATS)

　　其实我本身没有负责这个项目的测试，不过是不想闲着所以拿这个做做玩玩：）有这样一个弹出窗口，上面有很多CheckBox，我只选了其中的7个作为例子的测试对象，意在举例子。

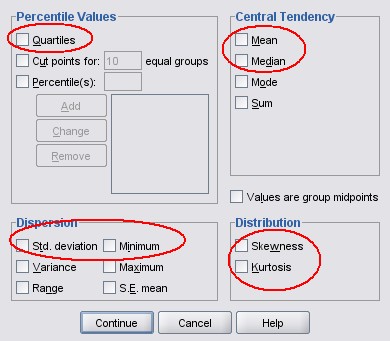
　　下表提取出需要测试的7个对象，他们分别有两种状态，要么被选中没有没有被选中：

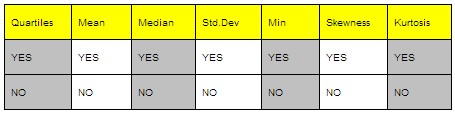
　　然后根据正交表进行映射，可以得到如下表，这个表有一部分是空的，那是因为用这8个case表示的两两组合已经是符合正交表的低要求，是两两组合至少出现一次，所以有这样子的空位出现

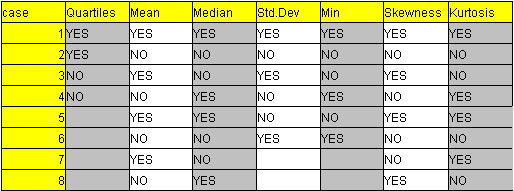
　　在处理这些空的数据格的时候我们可以根据一条原则进行处理，是对那些敏感的区域或者是你觉得出现bug机会比较大的情况进行检验。例如下表，我假定Quartiles是选中的状态下有可能出现bug，所以我把这4个空全部填上了YES。对于后面那两个字段也是采用了同样的处理方法。得出了下面这个表。

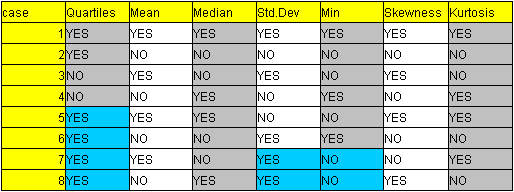
　　对于有7个字段，每个字段有2种可能的数值的情况，如果要做一个全面的测试，需要2的7次方 128个Test Case来做一个全面的覆盖，但是如果加上其他字段，或者某些字段的可选值是很多的（例如一个Text Box，用等价类划分了以后可能也有4~5种）。做一个全面的测试是不可能的。现在用8个测试用例来替代原来128个的方案，虽然肯定不能保证做到发现全部的bug，不过我个人觉得是一个“性价比”比较高的方案。

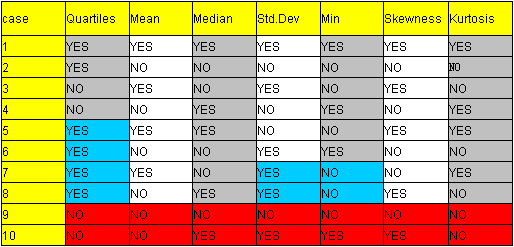
　　当然了，我们不能完全依靠正交表，如果不是我们本身的价值哪里去了，其实观察一下上面的表，很容易地发现了上面的表是没有全部NO的Test Case的，所以我们可以根据自己的经验，认为全部都不选的情况是一个比较常见而且有肯能出错的情况，所以加上，然后还能加上一些在软件实际使用过程当中比较常用的组合还有容易出错的组合，来完成这个Test Case计划。见下表，红色的是后来加上去的。