在提出了边界值测试以后为什么还要提出等价类测试？自相琢磨一下边界值测试的问题。

　　第一：边界值测试的测试用例过分冗余。举个例子来说，三角形问题假设每个边的范围是[1，200]，肯定会至少存在如下的三个测试用例：<1，1，1>和<100，100，100>还肯定会有<200，200，200>，看到这三个测试用例我们自然会很敏感的想到，这三个测试用例的数据特点决定了这三个测试用例应该是走的一样的流程，也是说后两个测试用例应该不会比第一个测试用例再测出什么新的问题来。所以这三个测试用例至少存在两个是冗余的。

　　第二：测试的完备性。也是说测试用例是不是能够覆盖到所有的情况上来。仔细考虑一下三角形边界值取值{不考虑坏情况的边界值测试，因为不是单缺陷假设}，所产生的测试用例是否覆盖了"不等边三角形"这种情况。答案是显然的，边界值测试在测试的完备性上也是有问题的。

　　因此基于上述所阐述的情况之下，提出了等价类测试。

　　通过上述的第一个阐述，应该可以建立起一个等价类的初步印象，我们试图将所有的测试用例划分成不同的等价类，利用每个等价类中的一个测试用例来代表这个等价类中的其他所有测试用例。如一所述<1，1，1>、<100，100，100>、<200，200，200>可以认为是一组等价类，我们只要用一个测试用例可以取代这一组类中所有的测试用例了。

　　在阐述等价类的几种测试模型之前，先搞清楚两个概念：强/弱，一般/健壮

　　在等价类测试当中，强指的是多缺陷假设，而弱指的是单缺陷假设，前者表明了一个笛卡尔乘积的概念

　　在等价类测试当中，一般指的是正常值，即不需要考虑异常者，而健壮性则刚好相反。

　　弱一般等价类测试(单缺陷假设，不讨论异常区域)

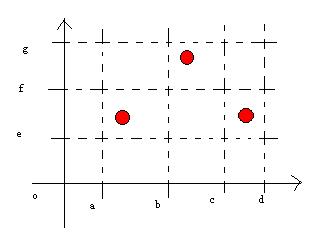
　　如上图所示，很显然，横坐标分为三个等价类[a，b]、[b，c]、[c，d]，而纵坐标分为二个等价类[g，f]、[f，e]，其中大于g小于“e”和大于“d”小于“a”的区域称为异常区域。再结合这个模型的名字来考虑，弱一般等价类，首先弱说明这是个单缺陷假设，所以不需要进行笛卡尔积的测试，第二方面是一般性的等价类，也是说不会测试异常区域。下面我们来看下三个红点所代表的意义(从左往右)，第一个红点测试了[a，b]和[e，f]区域，而第二个红点测试了[g，f]和[b，c]两个等价类区域，经过这两个测试用例很显然还有一个等价类区域没有进行测试，那是[c，d]区域，为了测试这个区域我们便有了第三个红点，这个红点在[f，e]或者[g，f]区域都没有关系，因为他主要测试的是[c，d]这个域。这便是弱一般等价类测试的用例数，一共三个。