量化项目管理案例：缺陷趋势预测利器（5)

作者：网络转载发布时间：[ 2011/10/28 14:20:59 ] 推荐标签：

S型可靠性增长模型还有2种特殊形式：

1. Delay-S型可靠性增长模型

Delay-S型可靠性增长模型也叫做延迟S型可靠性增长模型。

对于软件缺陷移除过程，测试过程应当不仅包括缺陷检测过程，还包括一个缺陷隔离过程。由于故障分析需要一定的时间，这个时间应当不是可以忽略不计的，在观察到的第一个故障时间和报告时间之间有很大的延迟。随时间观测到的延迟缺陷累计数符合S曲线分布，这种情况称为延迟S型曲线模型。

Delay-S型可靠性增长模型的函数形式
Delay-S的累积缺陷分布函数(CDF)：F(t)=K*(1-(1+λ*t)exp(-λ*t))；
Delay-S的缺陷概率密度函数(PDF)：f(t)=K*(λ^2)*t*exp(-λ*t)；
其中，t是时间，K是总缺陷数或者累积缺陷率。
Delay-S型可靠性增长模型对应的函数图

图3 Delay-S型曲线的CDF图

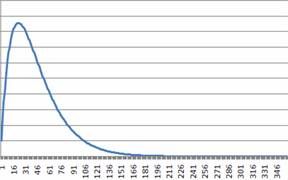
图4 Delay-S型曲线的PDF图

2. Inflection-S型可靠性增长模型

Inflection-S型可靠性增长模型也叫做变形S型可靠性增长模型。

变形S型可靠性增长模型用检测到的缺陷之间的相互依赖性描述了软件故障检测现象。具体来说，检测到的故障越多，有更多没有检测到的缺陷变得可以检测。这个模型讨论了缺陷之间的相互关系，可能与实际情况更接近。

Inflection-S型可靠性增长模型的函数形式
Inflection-S的累积缺陷分布函数（CDF）：F(t)=K*(1-exp(-λ*t))/(1+Φ*exp(-λ*t))；
Inflection-S的缺陷概率密度函数（PDF）：f(t)=K*λ*exp(-λ*t)*(1+Φ)/(1+Φ*exp(-λ*t))^2；
其中，t是时间，K是总缺陷数或者累积缺陷率。
Inflection-S型可靠性增长模型的曲线形式与普通S型曲线增长模型相似。
拟合度判断
在上一篇里，已经介绍了如何选择曲线模型，这一篇里，将会介绍怎样预测出该模型下符合实际数据的曲线，选择合适的模型。（模型的拟合算法将单独介绍）

给定一组实际数据，要让你预测出今后的一段时间，该数据的发展趋势，很多情况下，你并不能一下子找到符合这组数据发展趋势的模型。而实际上，又有太多模型可以选择，每一个模型都会得到一个不同的发展趋势。好比买衣服，琳琅满目、各式各样，可是，到底哪一件适合你要出席的场合呢？所以，到底是指数合适，还是Gompertz合适，又或者是Logistic合适呢？

这个时候，迫切的需要一个评判的标准，这种标准称为拟合度。拟合度的评价也有几种方法，本文列出了几种常用的拟合度判断方法，并对这几种方法进行总结、对比。

?利用相关系数R2来进行拟合度判断

相关系数R2是一种常见的拟合度的判断方法，常用于判断线性曲线的拟合度，然而在许多非线性曲线的拟合度判定过程中使用的依然是判断R2的方法，这个判断标准在实践中也被证明是符合实际的。实际中，R2较大的曲线模型，往往也是拟合较好的模型。

计算残差平方和Q=∑(y-y*)^2，其中，y代表的是实测值，y*代表的是预测值
计算相关系数R2=1-Q/∑(y-ya)^2，其中，y代表的是实测值，ya代表的是实测值的平均数
判断方式：R2越大、越接近1，认为拟合度越好
?利用变换的R2来进行拟合度判断??以Gompertz曲线和Logistic曲线为例

Gompertz曲线和Logistic曲线的预测过程（无论是三点法还是三和法）首先都需将模型的函数进行变换（对Gompertz模型进行对数变换，对Logistic模型进行倒数变换），然后再运用三和法或者三点法的原理进行计算。所以这里提出一种运用变换的相关系数R2来进行拟合度判断。

Gompertz曲线
分别将实测值和预测值进行对数变换
将对数变换后的实测值记作y，将对数变换后的预测值记作y*
根据相关系数的计算方法，计算变换后的残差平方和Q和相关系数R2
Logistic曲线
分别将实测值和预测值进行求倒数变换
将求倒变换后的实测值记作y，将求倒变换后的预测值记作y*
根据相关系数的计算方法，计算变换后的残差平方和Q和相关系数R2
?利用实测数据与拟合数据来进行拟合度判断

由于R2是用于判断线性模型的拟合程度的，对于非线性曲线，似乎不具有什么理论上的支持，所以，出现了许多针对非线性曲线进行的拟合度判定。下面的方法是其中的一种。

同样，计算残差平方和Q=∑(y-y*)^2和∑y^2，其中，y代表的是实测值，y*代表的是预测值
计算新的拟合度指标RNew=1-(Q/∑y^2)^(1/2)
判断方式：RNew越接近1，认为拟合度越好
?利用余弦函数进行辅助判断

从上一种方法中可以看出，在参数个数相同的前提下，拟合值越接近实测值，则认为拟合得越好。由此出现了根据几何意义得到的方法：若把实测值和预测值视为N维空间中的向量，若它们之间的夹角Θ越小，则可以认为拟合得越好。这里，计算角余弦系数FR=cosΘ=∑(yy*)/((∑y^2)^(1/2)* (∑y*^2)^(1/2))。

经实验证明，RNew的分辨率和灵敏度都较高，计算简单。实际中，可先用FR初选，再用RNew精选，可能会得到较好的结果。

平均偏差、平均平方误差、平均预测误差和平均百分误差

下面将介绍平均偏差、平均平方误差、平均预测误差和平均百分误差这四个评价指标。下面各指标中，At表示时段t的实际值，Ft表示时段t的预测值，n是整个预测期内的时段个数（或预测次数）。

?平均偏差MAD：Mean Absolute Deviation

平均偏差是整个预测期内每一次预测值与实际值的偏差(不分正负，只考虑偏差量)的平均值。

公式：MAD=(∑|At-Ft|)/n，t=1…n

MAD与标准偏差类似，但更容易求得。MAD能较好地反映预测的精度，但它不容易衡量无偏性。

?平均平方误差MSE：Mean Square Error

公式：MSE=(∑At-Ft)^2/n，t=1…n

MSE与MAD相似，可以较好的反映精度，但无法衡量无偏性。

?平均预测误差MFE：Mean Forecast Error

平均预测误差是指预测误差的和的平均值。