图1-4是应用这些图形符号绘制的一个较为简单的故障树形式。根据这种故障树，可以从选定的系统故障状态，即顶端事件开始，逐级地找出其上一级与下一级的逻辑关系，直至后追溯到那些初始的或其故障机理及故障概率为已知的，因而不需要继续分析的基本事件时为止。这样，可得出这个系统所有基本事件与其顶端事件之间的逻辑关系。在大多数情况下，故障树都是由与门及或门综合组成。因此，在各基本事件均为独立事件的条件下，即可利用事件的和、积、补等布尔代数的基本运算法则，列出这个系统的故障函数（系统故障与基本事件的逻辑关系）。随后，可进一步对顶端事件做出定性的或定量的分析。下面我们以图1-4所示的故障树为例，试用上述方法进行系统故障分析。

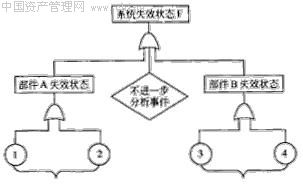
图1-4  故障树的形式
①，②，③，④--基本事件X1，X2，X3，X

图1-5  一项轴承故障分析的典型故障树
自或门；◇不完全事件；口与门；口事件；○基本事件；△事件转移

【例1】试分析图1-4所示的故障树，并列出该系统的故障函数。

解：由图可知，本例为一个两级故障树。即系统故障的顶端事件F是由第一级部件A的故障事件XA和部件B的故障事件XB的或门组成（图中还有一个菱形事件符号，表示该事件的原因未明或者对系统故障影响很小，可不予考虑），故有：F(x) =XA U XB的逻辑关系；而第二级则有由基本事件X1和X2组成的或门，还有由基本事件X3和X4所组成的或门。因此有：
XA= X1UX2及XB=X3∩X4；代入第一级关系式中得：F=XAUXB = (X1UX2）U(X3∩X4），故系统失效函数可简写为：F(x)=X1+X2+X3+X4

上式表示出了顶端事件即这个系统的故障与其四个基本事件X1，X2，X3，X4之间的逻辑关系。  图1-5是一个分析轴承事故的故障树例子。图中使用了三角形符号，其作用相当于一个注释符*，表示事件将由此转向标号相同的此类符号处继续展开。其目的是为了避免画面线太多造成分析上的困难。